A minimal model trained on synthetic data
This example will cover most steps of a systems biology problem on a small model and synthetic data. It will:
- Implement and simulate the model,
- evaluate a start guess of the parameter values,
- improve the values using optimization,
- gather the model uncertainty,
- predict a new experiment,
- and finally compare it to experimental data.
This section refers to an implementation of a model used in a computer exercise. We assume that the model below is saved in a file named M1.txt
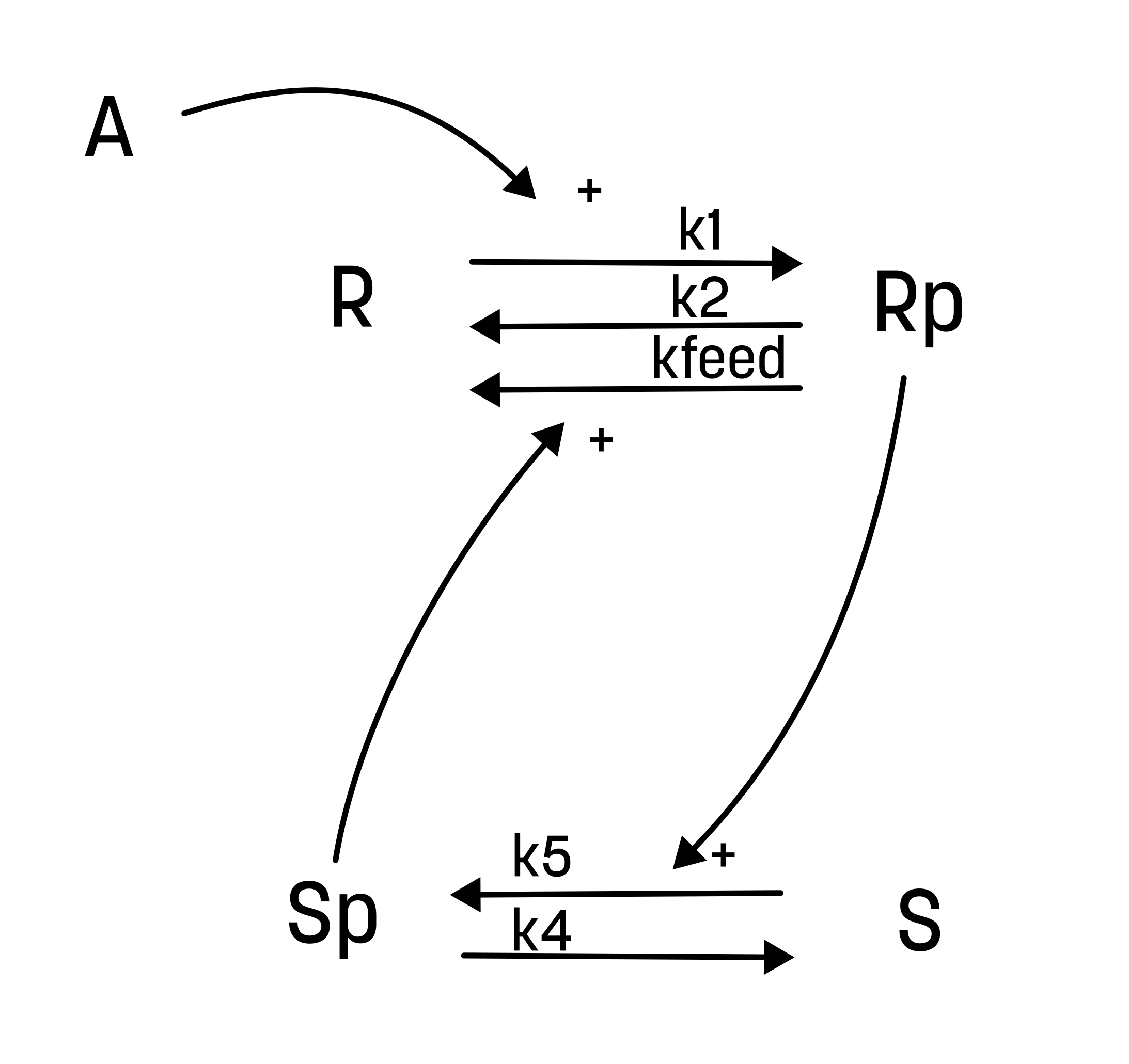
The model
########## NAME
M1
########## METADATA
timeunit = m
########## MACROS
########## STATES
d/dt(R) = r3+r2-r1
d/dt(Rp) = r1-r2-r3
d/dt(S) = r4-r5
d/dt(Sp) = r5-r4
R(0) = 1.0
Rp(0) = 0.0
S(0) = 1.0
Sp(0) = 0.0
########## PARAMETERS
k1 = 1.0
k2 = 0.0001
kfeed = 1000000.0
k4 = 1.0
k5 = 0.01
########## VARIABLES
r1 = R*A*k1
r2 = Rp*k2
r3 = Rp*Sp*kfeed
r4 = Sp*k4
r5 = S*Rp*k5
########## FUNCTIONS
########## EVENTS
########## OUTPUTS
########## INPUTS
A = A_in @ 1
########## FEATURES
y_sim = Rp
Step response inputs and integration issues
We need to add an event that internally resets the simulation when the input change happens. For this model, we can add two events which trigger when the A input changes value (A > 0 and A <= 0). Add the following under the EVENTS header:
event1 = A>0
event2 = A<=0
The Python code
Before you start, you should download the experimental dataset (right-click and save).
For this code to work, you need some packages (in addition to the SUND package). Install them with pip install numpy scipy matplotlib
#%% Import packages
import json
import csv
import random
import numpy as np
import matplotlib.pyplot as plt
import sund
from scipy.stats import chi2
from scipy.optimize import Bounds
from scipy.optimize import differential_evolution
#%% Load and print the data
with open("data_2024-03-12.json", "r") as f:
data = json.load(f)
# split the data into training and validation data
data_validation = {}
data_validation['step_dose'] = data.pop('step_dose')
print(data)
#%% Plot the data
def plot_dataset(data, FC='k'):
plt.errorbar(data['time'], data['mean'], data['SEM'], linestyle='None', marker='o', markerfacecolor=FC, color='k', capsize=5)
plt.xlabel('Time (minutes)')
plt.ylabel('Phosphorylation (a.u.)')
# Define a function to plot all datasets
def plot_data(data):
for idx, experiment in enumerate(data):
plt.figure(idx)
plot_dataset(data[experiment])
plt.title(f'EGFR - {experiment}')
plot_data(data)
#%% Install the model
sund.install_model('M1.txt')
print(sund.installed_models())
#%% Import the model class and create a model object
M1 = sund.import_model("M1")
m1 = M1() # Create a model object from the model class
#%% Create a activity objects
activity1 = sund.Activity(timeunit='m')
activity1.add_output(sund.PIECEWISE_CONSTANT, "A_in", t = data['dose1']['input']['A_in']['t'], f=data['dose1']['input']['A_in']['f'])
activity2 = sund.Activity(timeunit='m')
activity2.add_output(sund.PIECEWISE_CONSTANT, "A_in", t = data['dose2']['input']['A_in']['t'], f=data['dose2']['input']['A_in']['f'])
#%% Create simulation objects
m1_sims = {}
m1_sims['dose1'] = sund.Simulation(models = m1, activities = activity1, timeunit = 'm')
m1_sims['dose2'] = sund.Simulation(models = m1, activities = activity2, timeunit = 'm')
#%% Define two function to plot the model simulation and data
def plot_simulation(params, sim, timepoints, color='b', feature_to_plot='y_sim'):
# Setup, simulate, and plot the model
sim.simulate(time_vector = timepoints,
parameter_values = params,
reset = True)
feature_idx = sim.feature_names.index(feature_to_plot)
plt.plot(sim.time_vector, sim.feature_data[:,feature_idx], color)
def plot_sim_with_data(params, sims, data, color='b'):
for idx, experiment in enumerate(data):
plt.figure()
timepoints = np.arange(0, data[experiment]["time"][-1]+0.01, 0.01)
plot_simulation(params, sims[experiment], timepoints, color)
plot_dataset(data[experiment])
plt.title(f'EGFR - {experiment}')
#%% Plot the simulation given the initial parameter values, along with the data
params0_M1 = [1, 0.0001, 1000000, 1, 0.001] # = [k1, k2, kfeed, k4, k5]
plot_sim_with_data(params0_M1, m1_sims, data)
#%% Define a function to calculate the cost
def fcost(params, sims, data):
cost=0
for experiment in data.keys():
try:
sims[experiment].simulate(time_vector = data[experiment]["time"],
parameter_values = params,
reset = True)
y_sim = sims[experiment].feature_data[:,0]
y = data[experiment]["mean"]
SEM = data[experiment]["SEM"]
cost += np.sum(np.square(((y_sim - y) / SEM)))
except Exception as e:
# print(str(e)) # print exception, not generally useful
cost+=1e30 # in-case of exception add a "high cost"
return cost
#%% Improving the agreement manually
param_guess_M1 = [1, 0.0001, 1000000, 1, 0.01] # Change the values here and try to find a better agreement
cost = fcost(param_guess_M1, m1_sims, data)
print(f"Cost of the M1 model: {cost}")
dgf=0
for experiment in data:
dgf += np.count_nonzero(np.isfinite(data[experiment]["SEM"]))
chi2_limit = chi2.ppf(0.95, dgf)
print(f"Chi2 limit: {chi2_limit}")
print(f"Cost > limit (rejected?): {cost>chi2_limit}")
plot_sim_with_data(param_guess_M1, m1_sims, data)
#%% Improving the agreement using optimization methods
def callback_M1(x,convergence):
with open("./M1-temp.json",'w') as file:
out = {"x": list(x)}
json.dump(out,file)
args_M1 = (m1_sims, data)
#%% Convert to log scale
x0_log_M1 = np.log(param_guess_M1)
bounds_M1_log = Bounds([np.log(1e-6)]*len(x0_log_M1), [np.log(1e6)]*len(x0_log_M1)) # Create a bounds object needed for some of the solvers
def fcost_log(params_log, sim, data):
params = np.exp(params_log.copy())
return fcost(params, sim, data)
def callback_M1_log(x,convergence):
callback_M1(np.exp(x.copy()),convergence)
res = differential_evolution(func=fcost_log, bounds=bounds_M1_log, args=args_M1, x0=x0_log_M1, callback=callback_M1_log, disp=True) # This is the optimization
res['x'] = np.exp(res['x']) # convert back from log scale
print(f"\nOptimized parameter values: {res['x']}")
print(f"Optimized cost: {res['fun']}")
print(f"chi2-limit: {chi2_limit}")
print(f"Cost > limit (rejected?): {res['fun']>chi2_limit}")
if res['fun'] < chi2_limit: #Saves the parameter values, if the cost was below the limit.
file_name = f"M1 ({res['fun']:.3f}).json"
with open(file_name,'w') as file:
res['x'] = list(res['x']) #We save the file as a .json file, and for that we have to convert the parameter values that is currently stored as a ndarray into a traditional python list
json.dump(res, file)
#%% Plot the simulation given the optimized parameters
p_opt_M1 = res['x']
plot_sim_with_data(p_opt_M1, m1_sims, data)
#%% Setup for saving acceptable parameters
all_params_M1 = [] # Initiate an empty list to store all parameters that are below the chi2 limit
def fcost_uncertainty_M1(param_log, model, data):
param = np.exp(param_log) # Assumes we are searching in log-space
cost = fcost(param, model, data) # Calculate the cost using fcost
# Save the parameter set if the cost is below the limit
if cost < chi2.ppf(0.95, dgf):
all_params_M1.append(param)
return cost
#%% Run the optimization a few times to save some parameters
for i in range(0,5):
res = differential_evolution(func=fcost_uncertainty_M1, bounds=bounds_M1_log, args=args_M1, x0=x0_log_M1, callback=callback_M1_log, disp=True) # This is the optimization
x0_log_M1 = res['x']
print(f"Number of parameter sets collected: {len(all_params_M1)}") # Prints now many parameter sets that were accepted
#%% Save the accepted parameters to a csv file
with open('all_params_M1.csv', 'w', newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerows(all_params_M1)
#%% Plot model uncertainty
# Define a function to plot the model uncertainty
def plot_uncertainty(all_params, sims, data, c='b', n_params_to_plot=500):
random.shuffle(all_params)
for idx, experiment in enumerate(data):
# Plot the simulations
plt.figure(idx) # Create a new figure
timepoints = np.arange(0, data[experiment]["time"][-1]+0.01, 0.01)
for param in all_params[:n_params_to_plot]:
plot_simulation(param, sims[experiment], timepoints, c)
# Plot the data
plot_dataset(data[experiment])
plt.title(f'EGFR - {experiment}')
# Plot the uncertainty for the model
plot_uncertainty(all_params_M1, m1_sims, data)
#%% Setup for simulating the new prediction
m1_pred_sims = {}
for key, value in data_validation.items():
print(value)
act_prediction = sund.Activity(timeunit='m')
act_prediction.AddOutput(name = "A_in", type = sund.PIECEWISE_CONSTANT, tvalues=value["input"]["A_in"]["t"], fvalues = value["input"]["A_in"]["f"])
m1_pred_sims[key] = sund.Simulation(models = m1, timeunit = 'm', activities = act_prediction)
#%% Plot model predict with the experimental data
plot_uncertainty(all_params_M1, m1_pred_sims, data_validation)
plt.show()